➕➖ mathy ➗✖️

Welcome!✌ I write math stuff here.

☀️

🌒

Latin Standard

Libertinus

Geometri Susah dari Simulasi OSN 2017 by KTOM

Published on 3 January 2023. Posted originally in 2018 here, reposted with some changes

Pada Simulasi OSN 2017 versi KTOM, soal nomor empatnya adalah geometri. Sudah menjadi rahasia umum bahwa pada penyelenggaraan OSN Matematika, soal-soal disusun tingkat kesulitannya dari yang (dianggap) paling mudah hingga yang (dianggap) paling susah pada tiap hari. Dengan kata lain, soal nomor empat dan nomor delapan OSN (seharusnya) merupakan dua soal yang paling susah.

Dan jujur, soal yang satu ini bener-bener susah 😦

Pertama kali saya lihat soal ini tentu saja ketika Simul OSN ’17 KTOM-nya sedang berlangsung. Waktu itu saya tidak bisa mengerjakannya dan menyerah. Saya tidak ingin menanyakan solusinya terlebih dahulu agar soal ini dapat di-attempt lagi. Sayangnya seiring waktu soal ini malah terlupakan. Sepertinya soal ini akan benar-benar unsolved oleh saya untuk selamanya 😥

Akan tetapi takdir berkata lain. Tempo hari, ada yang nanya ke saya soal ini. Akhirnya saya dipertemukan kembali dengan si soal. Saya kerjain lagi deh.

Setelah setahun, akhirnya soalnya solved! Yey :0

Problem Statement

Diberikan segitiga $XYZ$ yang memenuhi $XY \neq XZ$. Misalkan lingkaran singgung luar segitiga $XYZ$ yang berseberangan terhadap $X$ (katakan lingkaran tersebut $\omega$) menyentuh $YZ$, $ZX$ dan $XY$ berturut-turut di $U$, $V$, dan $W$. Misalkan $R$ dan $S$ berturut-turut adalah titik pada segmen $XZ$ dan $XY$ sedemikian sehingga $RS$ dan $YZ$ sejajar, dan misalkan $\Gamma$ adalah lingkaran yang melewati $R$ dan $S$ dan bersinggungan di luar terhadap $\omega$ di $T$. Buktikan bahwa $VW$, $UT$, dan $RS$ bertemu di satu titik.

Solusi

Lemma untuk solusi

Lemma Diberikan dua lingkaran $O_1$ dan $O_2$. Pilih titik $C$ pada $O_1$ dan $A$, $B$ pada $O_2$ sehingga $CA$, $CB$ menyinggung $O_2$. Segmen $CA$, $CB$ masing-masing memotong $O_1$ berturut-turut di $D$, $E$. Misalkan $F = DE \cap AB$. Maka, radical center dari tiga lingkaran $O_1$, $O_2$, dan lingkaran radius nol berpusat di $F$ terletak pada garis $DE$.

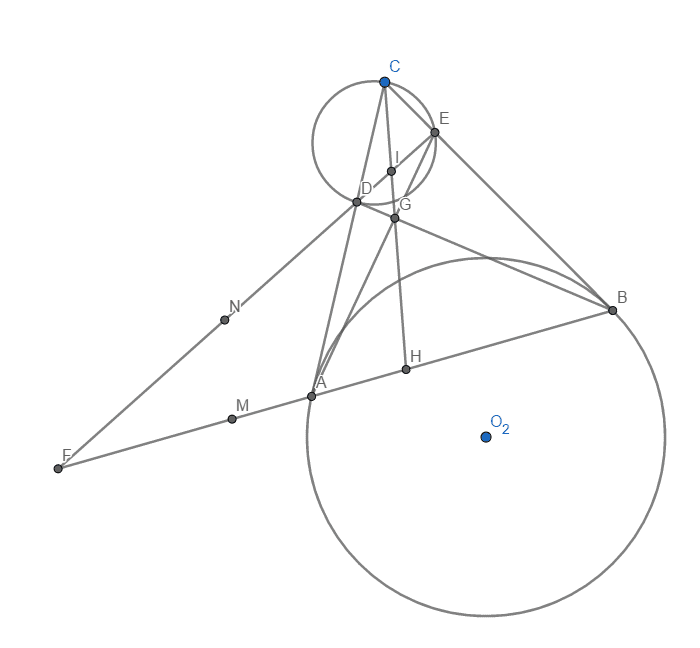
Bukti lemma Notasikan: $G = BD \cap AF$, $H = CG \cap AB$, $I = CG \cap DE$, $M$ sebagai titik tengah $FH$ dan $N$ sebagai titik tengah $FI$. Perhatikan bahwa berdasarkan Menelaus dan Ceva:\[ (E,D;I,F) = (B,A;H,F) = -1 \]Berdasarkan Teorema La Hire, karena $F$ terletak pada $AB$, yang merupakan polar $C$ terhadap lingkaran $O_2$, maka $C$ terletak pada polar $F$ terhadap lingkaran $O_2$. Selain itu, karena $(B,A;H,F) = -1$, maka $H$ terletak pada polar $F$ terhadap lingkaran $O_2$ juga. Maka, $CH$ merupakan polar $F$ terhadap lingkaran $O_2$. Maka, $O_2F \perp CH$. Berdasarkan definisi $M$ dan $N$, kita tahu bahwa $MN \parallel CH$. Maka, $O_2F \perp MN$.Berdasarkan properti harmonic bundle (apalah namanya lol) kita punya:\[ MF^2 = MH^2 = MA \times MB \]Maka, $M$ terletak pada radical axis lingkaran $O_2$ dan lingkaran titik $H$ radius nol. Karena $MN$ tegak lurus dengan garis yang menghubungkan kedua pusat lingkaran tersebut (yaitu $O_2F$), maka $MN$ adalah radical axis dari lingkaran $O_2$ dan lingkaran titik $H$ radius nol. Padahal, dengan sifat harmonik yang sama, kita juga punya:\[ NF^2 = NI^2 = ND \times NE \]Akibatnya, $N$ terletak pada radical axis lingkaran $O_1$ dan lingkaran titik $H$ radius nol. Dari sini, kita simpulkan bahwa $N$ adalah radical center dari ketiga lingkaran. $\blacksquare$

Solusi

Kita kembali ke soal dan gunakan lemma di atas untuk $C=X$, $O_2 = \omega$, $D=R$ dan $E=S$. Maka, ini berakibat $A=V$ dan $B=W$. Misalkan $J = RS \cap VW$. Notasikan $K$ sebagai radical center dari lingkaran-lingkaran $XRS$, $\omega$, dan lingkaran radius nol di $J$. (Pada gambar di lemma di atas, $K=N$) Dari titik $K$, buat garis singgung ke lingkaran $\omega$ di $L$. Misal $JL \cap \omega = U'$. Terakhir, cukup dibuktikan garis singgung $\omega$ pada $U'$ sejajar dengan $RS$ (mengapa?). Ini tidak sulit dengan memperhatikan bahwa $KJ = KL$. $\square$

Remark Lemma-nya mau saya propose ke OSN 2018, tetapi sayangnya sudah pernah saya kasih lihat ke adek kelas. Jadinya saya propose soal lain, dan walaupun nggak masuk di OSN 2018, turns out soal tersebut dipakai di pelatnas setelahnya.